高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型．在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉，小木钉之间留有适当的空隙作为通道，前面挡有一块玻璃．将一个小球从顶端放入，小球下落的过程中，每次碰到小木钉后都等可能地向左或向右落下，最后落入底部的格子中．格子从左到右分别编号为 $1,2, \ldots, 7$ ，用 $X$ 表示小球最后落入格子的号码。

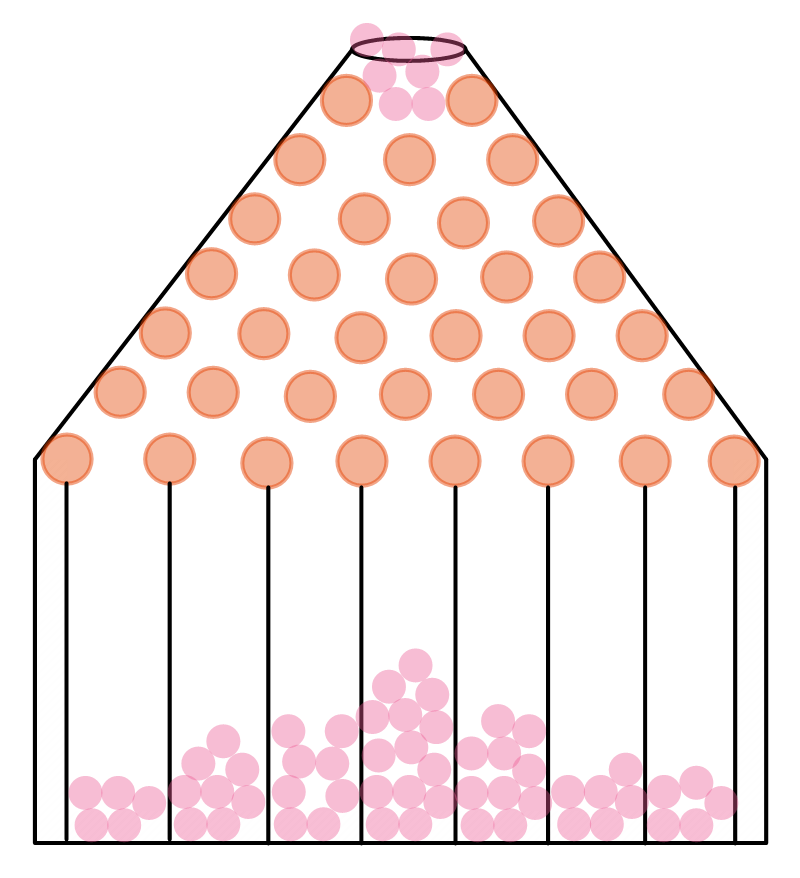
（1）求 $X$ 的分布列；
（2）小州同学在研究了高尔顿板后，想利用该图中的高尔顿板在学校社团文化节上进行盈利性＂抽奖＂活动．若 $2$ 元可以玩一次高尔顿板游戏，小球掉入 $X$ 号格子得到的奖金为 $Y$ 元，其中 $Y=\left\{\begin{array}{l}10, X=1 \text { 或 } 7 \\ 5, X=2 \text { 或 } 6 \\ 1, X=3 \text { 或 } 5 \\ 0, X=4\end{array}\right.$, 你觉得小州同学能盈利吗？